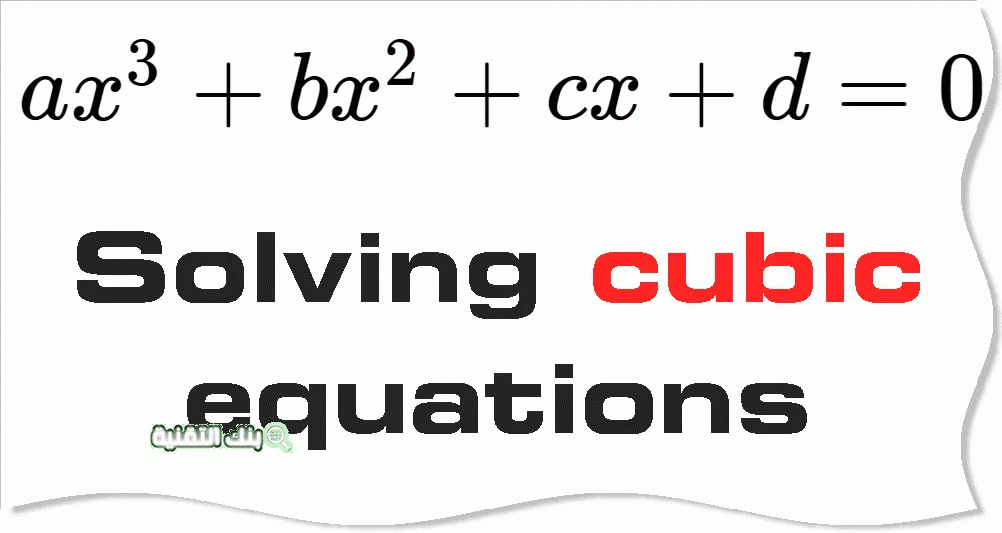كيفية حل معادلة من الدرجة الثالثة

نقدم لكم في مقالنا طريقة حل معادلة من الدرجة الثالثة والقانون العام لحل المعادلة التكعيبية وخطوات الحل وكذلك تمارين معادلات من الدرجة الثالثة واستخدام القسمة الاقليدية في الحل.

يمكنك الاطلاع على مقال حل معادلة من الدرجة الثالثة اون لاين حيث يمكنكم حل معادلة بشكل مباشر عن طريق إدخال العوامل في البرنامج.

الصيغة العامة للمعادلة من الدرجة الثالثة

تعطى الصيغة العامة للمعادلة التكعيبية من الدرجة الثالثة وفق ما يلي:

f(x) = ax3 + bx2 + cx + d = 0

تعبر x عن القيمة المجهولة التي من أجلها يكون هناك حل للمعادلة أو مجموعة حلول للتابع.

ومن شروط المعادلة التكعيبية أن تكون a≠0 بينما نسمي كلا من a, b, c, d معاملات المعادلة وهي أرقام حقيقة أي في مجموعة الأعداد الحقيقية.

خطوات حل معادلة من الدرجة الثالثة

فيما يلي الخطوط العامة لخطوات حل المعادلة من الدرجة الثالثة أو المعادلة التكعيبية وفي الفقرة التالية أمثلة وتمارين:

1. اختصار المعادلة أو إعادة تهيئتها:
   يتضمن اختصار المعادلة التخلص من جميع القيم القابلة للجمع أو الاختصار بجمع الأعداد مع بعضها وجمع أمثال x مع بعضها ونقلها لطرف واحد. ونفس الأمر على أمثال X2 أو X3.
2. تحديد رتبة المعادلة:
   بعد الاختصار يجب أن تبقى لدينا x3 اي أن أمثال x3 لا يجب أن يساوي الصفر وإلا فإن المعادلة ليست تكعيبية.
3. اختيار إحدى طرق الحل:
   بعد اختصار المعادلة وتهيئتها نختار أحد طرق الحل إما بطريقة كاردان أو القسمة الاقليدية أو تجميع المعادلة إلى أقواس.. الخ.

ملاحظة: يتيح موقع ويكي العربية برامج متنوعة لحل المعادلات الرياضية والهندسية وغيرها.

تمارين معادلات من الدرجة الثالثة

حل المعادلة من الدرجة الثالثة بطريقة العوامل المشتركة:

لتكن لدينا المعادلة التكعيبية التالية:

3x3 – 2x2 – x + 2 = 2x3

الحل: نقوم بنقل 2x3 إلى الطرف الأول

3x3 -2x3 – 2x2 – x + 2 = 0

x3 – 2x2 – x + 2 = 0

يمكن إخراج  x2 كعامل مشترك

⇒ x2(x – 2) – (x – 2) = 0

والآن يمكننا إخراج القوس (x – 2) كاملا كعامل مشترك

⇒ (x2 – 1)(x – 2) = 0

والآن وفقا لقوانين المساواة بين الطرفين فإما القوس الأول  x2 – 1 = 0 

x2 – 1 = 0

⇒x2 = 1 

⇒x1 = +1 , x2= -1

أو القوس الثاني يساوي الصفر

x-2 = 0 ⇒ x3 = 2

حل معادلة من الدرجة الثالثة بطريقة التحليل إلى عوامل

مفتاح حل المعادلة هو المعامل d حيث نحاول إيجاد القواسم المشتركة للمعامل ونجربها كحلول للمعادلة التكعيبية من الدرجة الثالثة. فإن كان إحداها صحيحا فهو حل للمعادلة وسنخبركم بالباقي في المثال:

 ليكن لدينا التابع التالي

f(x)=6x3−5x2−17x+6

نلاحظ المعامل d = 6 وبالتالي القواسم المشتركة له هي 1 و 2 و 3 و 6. لنجرب الرقم واحد كحل للمعادلة بتعويضه فيها:

f(1)=6(1)3−5(1)2−17(1)+6=6−5−17+6=−10

نستنتج أن الرقم 1 ليس حلا للمعادلة لان الناتج -10 ولا يساوي الصفر. لنجرب قاسما آخر وهو 2

f(2)=6(2)3−5(2)2−17(2)+6=48−20−34+6=0

نلاحظ أن الرقم 2 هو حل للمعادلة وبالتالي فإن القوس (x-2) هو أحد عوامل المعادلة.

الآن تتساءل عن الخطوة التالية والتي ستكون بتكهن أو استنتاج القوس التالي والذي إذا ضرب بالقوس (x-2) فلا تتغير المعادلة:

6x3−5x2−17x+6=(x−2)(6x2+7x−3)

 

الخطوة التالية هي بمتابعة تجميع الأقواس:

6x3−5x2−17x+6=(x−2)(2x+3)(3x−1)

وبالتالي فإن المعادلة تؤول للتالي:

(x−2)(2x+3)(3x−1) = 0

وبالتالي تكون جذور أو حلول المعادلة من الدرجة الثالثة هي:

x1 = 2

x2 = -3/2

x3 = ⅓

يمكنك أيضا الاطلاع على برنامج حل معادلة من الدرجة الثانية اون لاين.